
据吕梁三坐标测量机小编了解自牛顿在三百多年前首次确定了质量与引力之间的关系以来,科学家们一直致力于了解引力的力量。但是,万有引力常数G虽是人类最早认识的物理学基本常数,但亦是至今测量难度最大的常数,同时鉴于其应用国家最高水准的材料、机械、测量及控制技术,备受各国科学家的关注。
■ 精密扭秤
G之所以难以测量的部分原因在于与其他力相比它太微弱了,其值极小,约为6.67 × 10-11 m3 kg-1s-2,相当于电磁力的数万亿亿亿分之一。
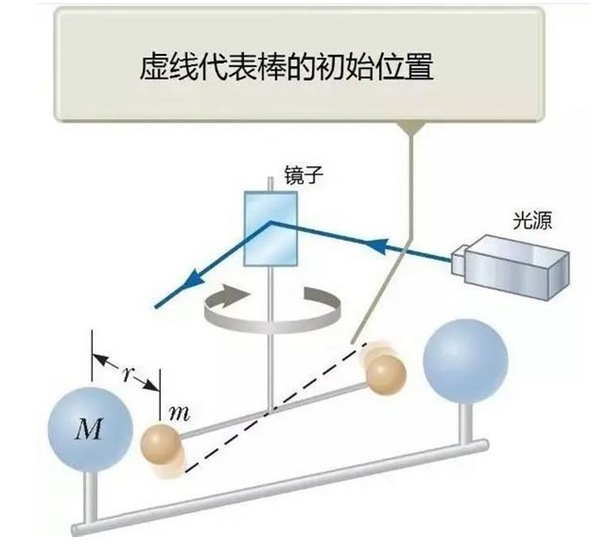
国际计量局(BIPM)在实验中使用一种精密扭秤测量G,此方法最早由英国科学家亨利·卡文迪许(Henry Cavendish)于1798年首次测量使用,此装置用以测量较小质量物体之间的引力,通常采用金属球体或圆柱体,实验中需测量金属悬丝或金属条的偏转或力矩等参数。
BIPM所使用的精密扭秤比卡文迪许原先使用的扭秤要复杂得多,其配置8个特殊合金圆柱体质量块,其中4个位于圆形转盘上,另外4个质量稍小的圆柱体位于转盘内的圆盘上,此圆盘通过一根2.5 mm宽、160 mm长、厚度相当于人类头发丝的铜铍金属丝悬挂于天平顶部。
此过程需将质量块固定于转盘外部,使其与转盘内部的质量块保持均衡,以达到平衡状态。当转盘外部的质量块转向一个新的方向时,转盘内部的质量块将感知一个微弱外力,该引力将导致内部质量块往外部质量块方向行进,使金属悬丝发生扭转,鉴于质量块之间的引力垂直于地球的重力,实验中地球的重力不会影响测量值。
由于将金属悬丝偏转一定角度所需力的大小为已知。因此,基于激光及金属悬丝顶部的镜子,科学家可测量内部质量块向固定的外部质量块行进的物理距离,从而计算它们之间的万有引力。
■ 实时几何量坐标测量
其中,测量大G的科研人员需测量牛顿引力方程中的其他量值,获取其所有零部件的精确尺寸及位置信息,“包括每个孔位、每个面形及每个装配件,”据NIST研究人员斯特林所述,“这皆需借助于三坐标测量机(CMM)”。

自20世纪后半叶,与科学史上其他时期相比,人类进行了更多的测量引力常数的研究工作。自1969年国际科技数据委员会(CODATA)成立以来,根据世界各地测G小组的最新实验结果,多次发布及调整万有引力常数G的推荐值。例如国际计量局(BIPM)在过去15年里进行的一组官方实验。尽管各个实验小组相继给出相对精度较高的测G实验结果,但它们之间的吻合程度仍然较差。
上图为大G测量的各项实验结果比对,其中垂直黑线表征G的最近推荐值,灰色区域表征误差区间
因此,如何进一步提高实验精度,寻找未知的系统误差,以及寻找新途径是测量万有引力常数G的发展趋势,两年前,BIPM科学家和世界上其他致力于测量大G的科学界领军人物齐聚一堂,决定这些测试实验重新用同一组设备、不同实验场所及不同的科研团队进行。
所以,三坐标测量机是工业产品数据测量和品质控制的关键设备,昆山友硕专注吕梁蔡司三坐标测针,蔡司三坐标测量仪、蔡司三维扫描仪销售与售后及应用解决方案十数年,更多关于蔡司三坐标的问题请咨询具体销售人员。











